[ML_Fairness]Fairness Definitions Explained

Table of Contents

Found at

Algorithm fairness has started to attract the attention of researchers in AI, Software Engineering and Law communities, with more than twenty different notions of fairness proposed in the last few years.
Yet, there is no clear agreement on which definition to apply in each situation.
Here in the paper, it intuitively explains why the same case can be considered fair according to some definitions and unfair according to others.

1. Introduction

AI now replaces humans at many critical decision points, such as who will get a loan [1] and who will get hired for a job [3]. One might think that these AI algorithms are objective and free from human biases, but that is not the case. For example, risk-assessment software employed in criminal justice exhibits race-related issues [4] and a travel fare aggregator steers Mac users to more expensive hotels [2]

The topic of algorithm fairness has begun to attract attention in the AI and Software Engineering research communities. In late 2016, the IEEE Standards Association published a 250-page draft docu- ment on issues such as the meaning of algorithmic transparency.

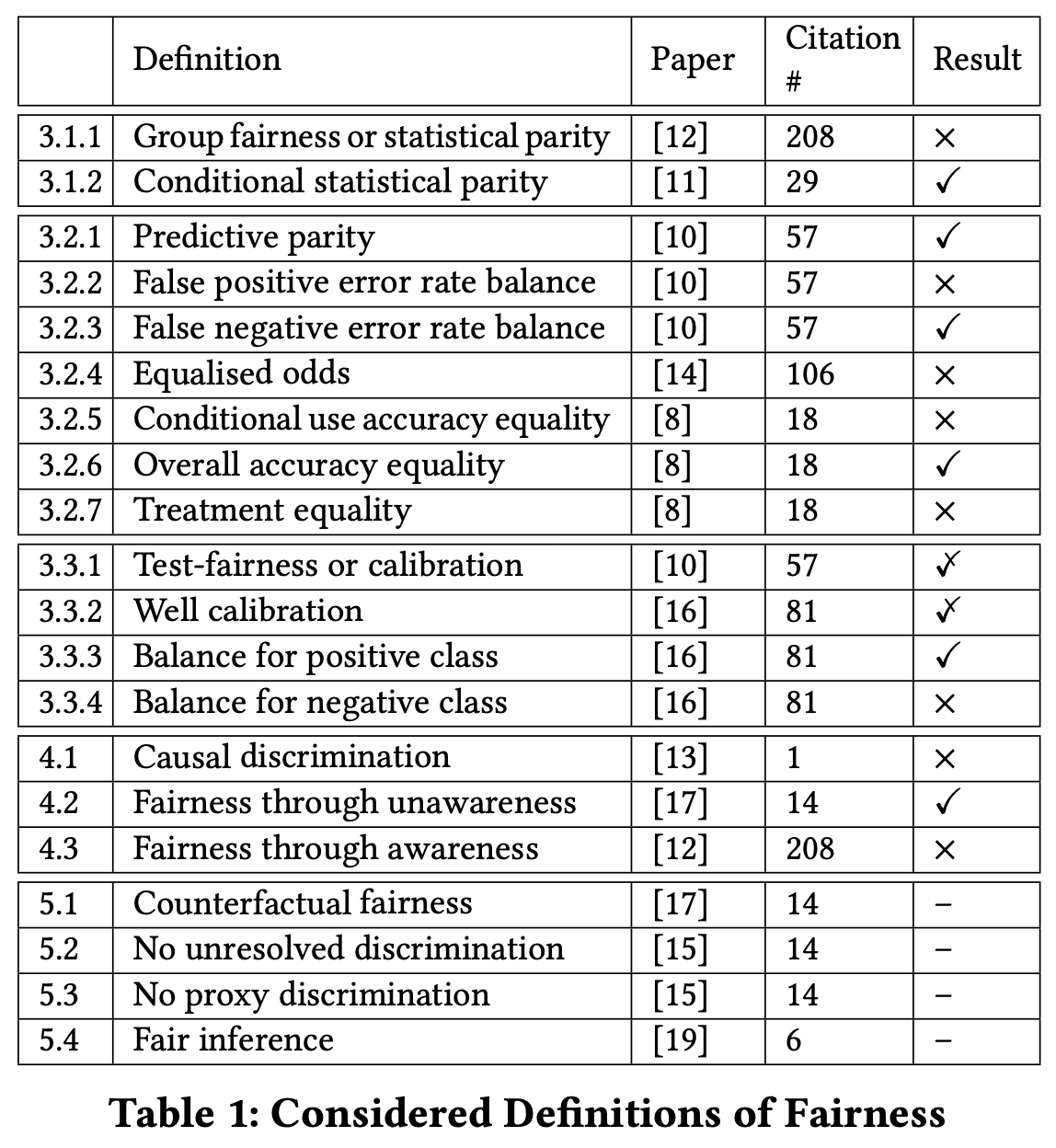
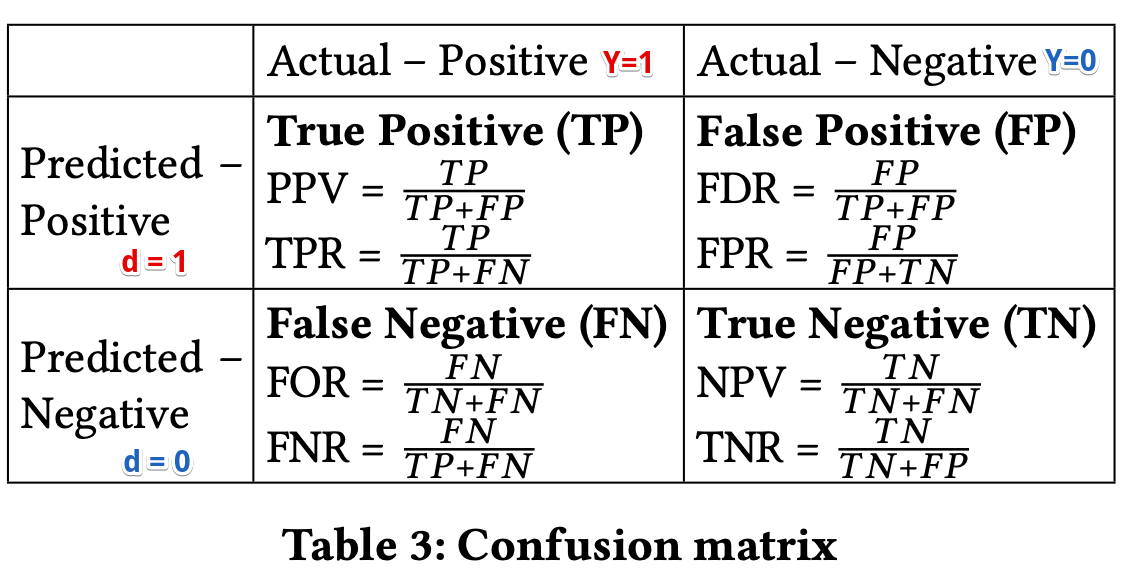
In this paper, we focus on the machine learning (ML) classification problem: identifying a category for a new observation given training data containing observations whose categories are known. We collect and clarify most prominent fairness definitions for clas- sification used in the literature, illustrating them on a common, unifying example – the German Credit Dataset This dataset is commonly used in fairness literature. It contains information about 1000 loan applicants and includes 20 attributes describing each applicant, e.g., credit history, purpose of the loan, loan amount requested, marital status, gender, age, job, and housing status. It also contains an additional attribute that describes the classification outcome – whether an applicant has a good or a bad credit score.

2. Background


© Verma et al.,

Above rows are definitions of ‘fairness’. All of them are papers. We will explain and see ‘fairness’ of algorithm from German Credit Dataset.

Heading is comprised of ‘#.#.#’ and the meaning is further explained below.
3.#.# STATISTICAL MEASURES
4.# SIMILARITY-BASED MEASURES
5.# CAUSAL REASONING

Notations

  • $G$ : Protected or sensitive attribute for which non-discrimination should be established.
  • $X$ : All additional attributes describing the individual.
  • $Y$ : (1 or 0) The actual classification result (here, good or bad credit score of an applicant as described in the dataset: attribute)
  • $S$ : Predicted probability for a certain classification. $=P(Y =c|G,X)$ (here, predicted probability of having a good or bad credit score).
  • $d$ : (1 or 0), Predicted decision (category) for the individual (here, predicted credit score for an applicant – good or bad); $d$ is usually derived from $S$, e.g., $d = 1$ when $S$ is above a certain threshold.

For example, the probability of having a good credit score ($S$) as established by a classifier is 88%. Thus, the predicted score ($d$) is good, same as the actual credit score recorded in the database ($Y$)

3. Statistical Measures

Confusion Matrix


© Verma et al.,


© Wikipedia

Notations

  • $TP$ : True Positive $P(Y=1, d=1)$
    • a case when the predicted and actual outcomes are both in the positive class.
  • $FP$ : False Positive $P(Y=0, d=1)$ a.k.a., Type 1 error
    • a case predicted to be in the positive class when the actual outcome belongs to the negative class.
  • $FN$ : False Negative $P(Y=1, d=0)$ a.k.a., Type 2 error
    • a case predicted to be in the negative class when the actual outcome belongs to the positive class.
  • $TN$ : True Negative $P(Y=0, d=0)$
    • a case when the predicted and actual outcomes are both in the negative class.

Ratios(Y: Actual, d: Predictive)

  • $PPV = \frac{TP}{TP+FP} = P(Y=1|d=1)$ , Positive Predictive Value
  • $FDR = \frac{FP}{TP+FP} = P(Y=0|d=1)$ , False Discovery Rate
  • $FOR = \frac{FN}{TN+FN} = P(Y=1|d=0)$, False Omission Rate
  • $NPV = \frac{TN}{TN+FN} = P(Y=0|d=0)$, Negative Predictive Value
  • $TPR = \frac{TP}{TP+FN} = P(d=1|Y=1)$, True Positive Rate
  • $FPR = \frac{FP}{FP+TN} = P(d=1|Y=0)$, False Positive Rate
  • $FNR = \frac{FN}{TP+FN} = P(d=0|Y=1)$, False Negative Rate
  • $TNR = \frac{TN}{FP+TN} = P(d=0|Y=0)$, True Negative Rate

3.1 Definitions Based on Predicted Outcome

3.1.1. Group Fairness

  • Also Known As “Statistical Parity”, “Equal Acceptance Rate” and “Benchmarking”.

Definition

A classifier satisfies this definition if subjects in both protected and unprotected groups have equal probability of being assigned to the positive predicted class.

\[P(d=1|G=m) = P(d=1|G=f)\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male

Applicants should have an equivalent opportunity to obtain a good credit score, regardless of their gender.

Consequence

The probability to have a good predicted credit score

  • 0.81 → married/divorced male
  • 0.75 → female

It is more likely for a male applicant to have good predicted score, so that we can deem classifier to fail in satisfying this definition of fairness.

3.1.2. Conditional Statistical Parity

Definition

Definition is satisfied if subjects in both protected and unprotected groups have equal probability of being assigned to the positive predicted class, controlling for a set of legitimate factors $L$.

As the examples of $L$, possible legitimate factors that affect an applicant creditworthiness could be the requested credit amount, applicant’s credit history, employment, and age.

\[P(d=1|L=l, G=m) = P(d=1|L=l,G=f)\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male
  • $L$ : Legitimate Factors

Consequence

The probability to have a good predicted credit score

  • 0.46 → Married/Divorced Male
  • 0.49 → Female

Unlike in the previous definition, here a female applicant is slightly more likely to get a good predicted credit score.

3.2 Definitions Based on Predicted and Actual Outcomes

3.2.1. Predictive parity

  • Also Known As “Outcome Test”.

Definition

A classifier satisfies this definition if both protected and unprotected groups have equal $PPV$ – the probability of a subject with positive predictive value to truly belong to the positive class.

Main idea behind this definition is that the fraction of correct positive predictions should be the same for both genders.

\[P(Y=1|d=1,G=m) = P(Y=1|d=1,G=f)\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male
  • $PPV = \frac{TP}{TP+FP} = P(Y=1|d=1)$ , Positive Predictive Value

Mathematically, a classifier with equal $PPV$s will also have equal $FDRs$ which are $P(Y = 0|d = 1,G = m) = P(Y = 0|d = 1,G = f)$.

Consequence

  • 0.73 → Married/Divorced Male
  • 0.74 → Female

The values are not strictly equal, but, again, we consider this difference minor, and hence deem the classifier to satisfy this definition.

3.2.2. False Positive Error Rate Balance

  • Also Known As “Predictive Equality”.

Definition

A classifier satisfies this definition if both protected and unprotected groups have equal $FPR$ – the probability of a subject in the negative class to have a positive predictive value.

The main idea behind this definition is that a classifier should give similar results for applicants of both genders with actual negative credit scores.

\[P(d = 1|Y = 0,G = m) = P(d = 1|Y = 0,G = f )\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male
  • $FPR = \frac{FP}{FP+TN} = P(d=1|Y=0)$, False Positive Rate

Mathematically, a classifier with equal $FPR$s will also have equal $TNR$s which are $P(d = 0|Y = 0,G = m) = P(d = 0|Y = 0,G = f)$.

Consequence

  • 0.70 → Married/Divorced Male
  • 0.55 → Female

The classifier is more likely to assign a good credit score to males who have an actual bad credit score; females do not have such an advantage and the classifier is more likely to predict a bad credit score for females who actually have a bad credit score. Classifier is deemed to fail in satisfying this definition of fairness.

3.2.3. False Negative Error Rate Balance

  • Also Known As “Equality Opportunity”.

Definition

A classifier satisfies this definition if both protected and unprotected groups have equal $FNR$ – the probability of a subject in a positive class to have a negative predictive value.

This implies that the probability of an applicant with an actual good credit score to be incorrectly assigned a bad predicted credit score should be the same for both male and female applicants

\[P(d = 0|Y = 1,G = m) = P(d = 0|Y = 1,G = f )\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male
  • $FNR = \frac{FN}{TP+FN} = P(d=0|Y=1)$, False Negative Rate

Mathematically, a classifier with equal $FNR$s will also have equal $TPR$ which are $P(d = 1|Y = 1,G = m) = P(d = 1|Y = 1,G = f )$.

Consequence

  • 0.14(0.86 for $TPR$) → Married/Divorced Male
  • 0.14(0.86 for $TPR$) → Female

This means that the classifier will apply equivalent treatment to male and female applicants with actual good credit score. Classifier is deemed to be satisfying this definition of fairness.

3.2.4. Equalized Odds

  • Also Known As “Conditional Procedure Accuracy Equality” and “Disparate Mistreatment”.

Definition

Definition combines the previous two: a classifier satisfies the definition if protected and unprotected groups have

  • equal $TPR$ and
  • equal $FPR$
\[P(d = 1|Y = i,G = m) = P(d=1|Y=i,G=f),i∈0,1.\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male
  • $TPR = \frac{TP}{TP+FN} = P(d=1|Y=1)$, True Positive Rate
  • $FPR = \frac{FP}{FP+TN} = P(d=1|Y=0)$, False Positive Rate

Consequence

$FPR$

  • 0.70 → Married/Divorced Male
  • 0.55 → Female

$TPR$

  • 0.86 → Married/Divorced Male
  • 0.86 → Female

This means that the classifier is more likely to assign a good credit score to males who have an actual bad credit score, compared to females. Hence the overall conjunction does not hold and we deem our classifier to fail in satisfying this definition.

3.2.5. Conditional Use Accuracy Equality

  • Also Known As “Conditional Procedure Accuracy Equality” and “Disparate Mistreatment”.

Definition

Definition combines the two: a classifier satisfies the definition if protected and unprotected groups have

  • equal $PPV$ and
  • equal $NPV$

This definition implies equivalent accuracy for male and female applicants from both positive and negative predicted classes. In our example, the definition implies that for both male and female applicants, the probability of an applicant with a good predicted credit score to actually have a good credit score and the probability of an applicant with a bad predicted credit score to actually have a bad credit score should be the same.

\[P(Y=1|d=1,G=m)=P(Y=1|d=1,G=f))∧(P(Y= 0|d=0,G=m)=P(Y=0|d=0,G=f)\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male
  • $PPV = \frac{TP}{TP+FP} = P(Y=1|d=1)$ , Positive Predictive Value
  • $NPV = \frac{TN}{TN+FN} = P(Y=0|d=0)$, Negative Predictive Value

Consequence

$PPV$

  • 0.73 → Married/Divorced Male
  • 0.74 → Female

$NPV$

  • 0.49 → Married/Divorced Male
  • 0.63 → Female

It is more likely for a male than female applicant with a bad predicted score to actually have a good credit score. We thus deem the classifier to fail in satisfying this definition of fairness.definition.

3.2.6. Overall Accuracy Equality

  • Also Known As “Conditional Procedure Accuracy Equality” and “Disparate Mistreatment”.

Definition

A classifier satisfies this definition if

  • both protected and unprotected groups have equal prediction accuracy – the probability of a subject from either positive or negative class to be assigned to its respective class.

The definition assumes that

  • true negatives are as desirable as true positives.

In this example, this implies that the probability of an applicant with an actual good credit score to be correctly assigned a good predicted credit score and an applicant with an actual bad credit score to be correctly assigned a bad predicted credit score is the same for both male and female applicants.

\[P(d = Y,G = m) = P(d = Y,G = f )\]

where,

  • $Y$ : Actual Binary
  • $d$ : Predicted Binary
  • $f$ : Female
  • $m$ : Male

Consequence

  • 0.68 → Married/Divorced Male
  • 0.71 → Female

While these values are not strictly equal, for practical purposes we consider this difference minor, and hence deem the classifier to satisfy this definition

3.2.7. Treatment Equality

Definition

This definition looks at the ratio of errors that the classifier makes rather than at its accuracy. A classifier satisfies this definition if both protected and unprotected groups have an equal ratio of false negatives and false positives.

\[\frac{FN}{FP}(m) = \frac{FN}{FP}(f)\]

where,

  • $f$ : Female
  • $m$ : Male

Consequence

  • 0.56 → Married/Divorced Male
  • 0.62 → Female

a smaller number of male candidates are incorrectly assigned to the negative class ($FN$) and / or larger number of male candidates are incorrectly assigned to the positive class ($FP$). Classifier is deemed to fail in satisfying this definition of fairness.

3.3. Definition bases on Predicted Probabilities and Actual Outcome

  • This part considers the actual outcome $Y$ and the predicted probability score $S$.

3.3.1. Test-fairness

  • Also Known As “Calibration” and “Matching Conditional Frequencies”

Definition

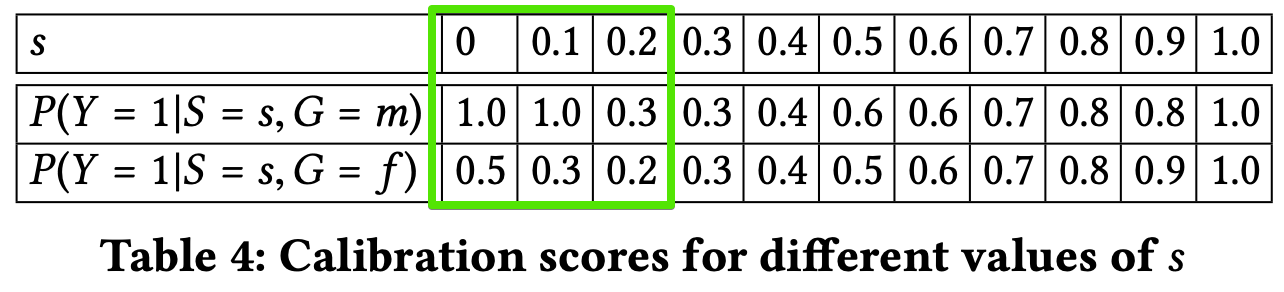
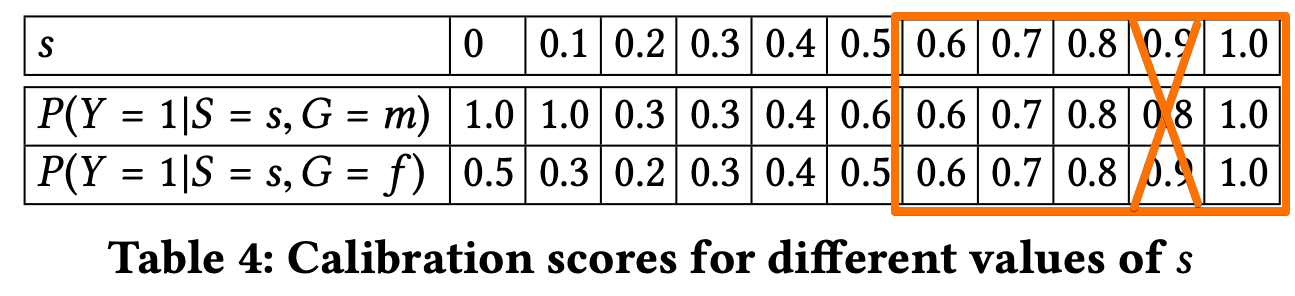
  • A classifier satisfies this definition if for any predicted probability score $S$, subjects in both protected and unprotected groups have equal probability to truly belong to the positive class.

  • This definition is similar to predictive parity (3.2.1), except that it considers the fraction of correct positive predictions for any value of $S$.
  • In our example, this implies that for any given predicted probability score $s$ in $[0, 1]$, the probability of having actually a good credit score should be equal for both male and female applicants:

\(P(Y = 1|S = s,G = m) = P(Y = 1|S = s,G = f )\) where,

  • $f$ : Female
  • $m$ : Male
  • $S$ : Predicted Probability Score $\in [0,1]$


© Verma et al.,

  • Table 4 shows the scores for male and female applicants in each bin. The scores are quite different for lower values of S and become closer for values greater than 0.5. Thus, classifier satisfies the definition for high predicted probability scores but does not satisfy it for low scores.
  • This is consistent with previous results showing that it is more likely for a male applicant with a bad predicted credit score (low values of S) to actually have a good score (definition 3.2.5), but applicants with a good predicted credit score (high values of S) have an equivalent chance to indeed have a good credit score, regardless of their gender (definition 3.2.1).

3.3.2. Well-Calibration

Definition

  • This definition extends the previous one(3.3.1. Test Fairness) stating that, for any predicted probability score $S$, subjects in both protected and unprotected groups should not only have an equal probability to truly belong to the positive class, but this probability should be equal to $S$.
  • That is, if the predicted probability score is $s$, the probability of both male and female applicants to truly belong to the positive class should be $s$

\(P(Y = 1|S = s,G = m) = P(Y = 1|S = s,G = f ) = s\) where,

  • $f$ : Female
  • $m$ : Male
  • $S$ : Predicted Probability Score $\in [0,1]$


© Verma et al.,

  • According to Table 4., classifier is well-calibrated only for $s ≥ 0.6$. Classifier is deem to be partially satisfing this fairness definition.

3.3.3. Balance for Positive Class

Definition

  • A classifier satisfies this definition if subjects constituting positive class from both protected and unprotected groups have equal average predicted probability score $S$
  • Violation of this balance means that one group of applicants with good credit score would consistently receive higher probability score than applicants with a good credit score from the other group.

\(E(S |Y = 1, G = m) = E(S |Y = 1, G = f ).\) where,

  • $f$ : Female
  • $m$ : Male
  • $S$ : Predicted Probability Score $\in [0,1]$

Consequence

  • 0.72 → Married/Divorced Male
  • 0.72 → Female
  • Classifier is deemed to be satisfying this notion of fairness.
  • This result further supports and is consistent with the result for equal opportunity (3.2.3), which states that the classifier will apply equivalent treatment to male and female applicants with actual good credit score ($TPR$ of 0.86).

3.3.4. Balance for Negative Class

Definition

  • Flipped version of 3.3.3.
  • This definition states that subjects constituting negative class from both protected and unprotected groups should also have equal average predicted probability score $S$. \(E(S|Y = 0,G = m) = E(S|Y = 0,G = f )\) where,
  • $f$ : Female
  • $m$ : Male
  • $S$ : Predicted Probability Score $\in [0,1]$

Consequence

  • 0.61 → Married/Divorced Male
  • 0.52 → Female

On average, male candidates who actually have bad credit score receive higher predicted probability scores than female candidates. Classifier fails in satisfying this definition of fairness.

4. Similarity-Based Measures

  • Statistical definitions above largely ignore all attributes of the classified subject $X$ except the sensitive attribute $G$.
  • Such treatment might hide unfairness:
    • For example, if the same fraction of male and female applicants are assigned a positive score.
    • Yet, male applicants in this set are chosen at random,
    • while female applicants are only those that have the most savings.
    • Then, statistical parity will deem the classifier fair, despite a discrepancy in how the applications are processed based on gender
  • The following definitions attempt to address such issues by not marginalizing over insensitive attributes $X$ of the classified subject.

4.1. Causal Discrimination

Definition

A classifier satisfies this definition if it produces the same classification for any two subjects with the exact same attributes $X$. which is,

\[(X_f =X_m ∧ G_f !=G_m)→d_f =d_m\]

where,

  • $f$ : Female
  • $m$ : Male
  • $X$ : Other non-sensitive Attributes
  • $d$ : Predicted Binary

    Consequence

  • An identical individual of the opposite gender and compared the predicted classification for these two applicants.
  • 8.8% married / divorced male and female applicants, the output classification was not same.

Classifier fails in satisfying this definition

4.2. Fairness through Unawareness

Definition

  • A classifier satisfies this definition if no sensitive attributes $S$ are explicitly used in the decision-making process,

  • In this example, this definition implies that gender related features($S$) are not used for training the classifier, so decisions cannot rely on these features.
  • This also means that the classification outcome should be the same for applicants $i$ and $j$ who have the same attributes, $X$.
\[X: X_i = X_j → d_i = d_j\]

where,

  • $f$ : Female
  • $m$ : Male
  • $X$ : Other non-sensitive Attributes
  • $d$ : Predicted Binary

Consequence

  • Logistic regression model was trained without using any features derived from the gender attribute($S$).
  • Then, for each applicant in the testing set,identical individual of the opposite gender is generated,
  • and compared the predicted classification for these two applicants.
  • Our results show that the classification for all “identical” individuals that only differ in gender was identical.
  • This result also indicates that no other feature of the dataset is used as a proxy for gender;
  • otherwise, the classifier would have shown similar results as in case of causal discrimination

Classifier satisfies this definition

4.3. Fairness through Awareness

Definition

  • Fairness is captured by the principle that “similar individuals should have similar classification”.
  • The similarity of individuals is defined via a distance metric;
  • for fairness to hold, the distance between the distributions of outputs for individuals should be at most the distance between the individuals.

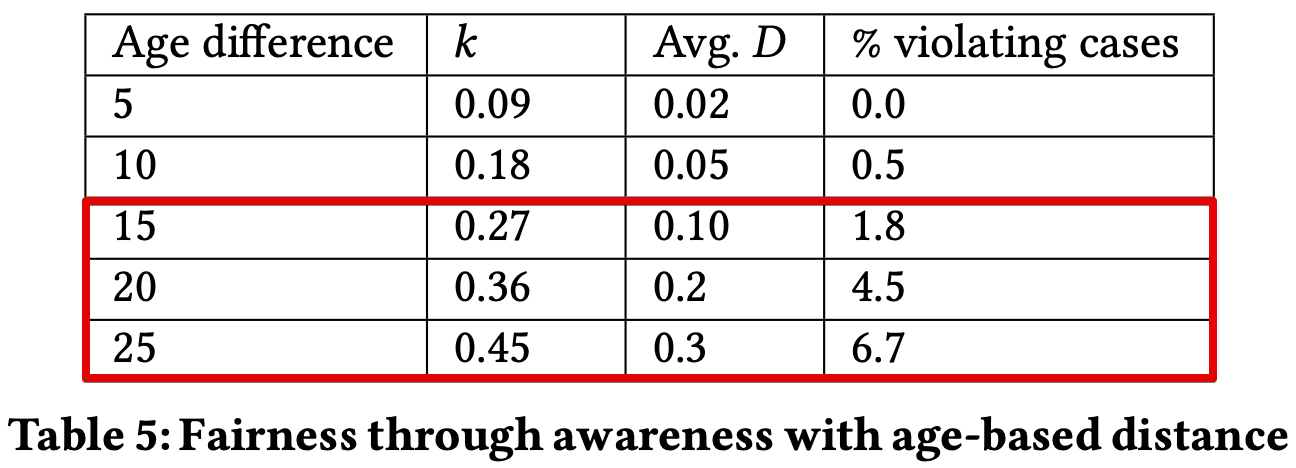
fairness is achieved if, \(D(M(x),M(y)) ≤ k(x,y)\)

where,

  • $V$ : Set of Applicants
  • $D$ : Distance Metric
  • $M$ : Function, $M: V \to \delta A$
  • $k$ : Distance Metric, $k: V * V \to R$

For example, mapping and distance metric can be defined as below. $k = \begin{cases} 0 &\text{if attributes in X (all attributes other than gender) are identical }
1 &\text{otw} \end{cases}$ and $D = \begin{cases} 0 &\text{if classifier resulted in the same prediction}
1 &\text{otw} \end{cases}$

or

$D(i, j) = S(i) - S(j)$

Consequence


© Verma et al.,

  • To test this, for each applicant in the testing set five additional individuals, with ages different by 5, 10, 15, 20 and 25 years(and identical otherwise), are generated.
  • Results in Table 5 show that the distance between outcomes (column 3) grew much faster than the distance between ages (column 2).
  • Thus, the percentage of applicants who did not satisfy this definition (column 4) increased.

For a smaller age difference, the classifier satisfied this fairness definition, but that was not the case for an age difference of more than 10 years.

5. Causal Reasoning


© Verma et al.,

  • $G$ : Protective Attribute
  • $ \text{Proxy}$ : An attribute whose value can be used to derive a value of another attribute
  • $ \text{Resolving Edge}$ : An attribute in the causal graph that is influenced by the protected attribute in a non-discriminatory manner

5.1. Counterfactual fairness

Definition

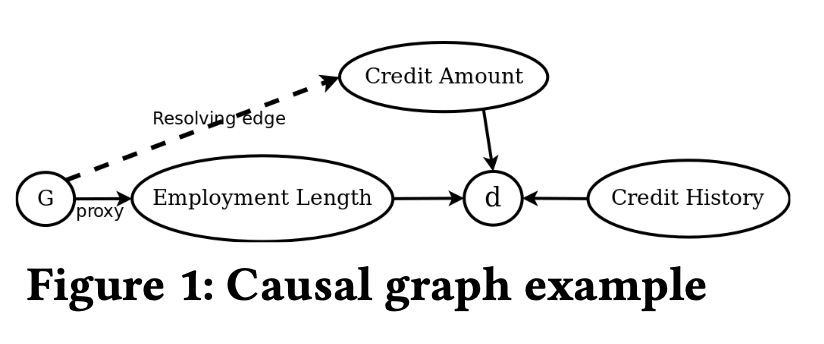
A causal graph is counterfactually fair if the predicted outcome $d$ in the graph does not depend on a descendant of the protected attribute $G$.

Consequence


© Verma et al.,

$d$ is a dependent on credit history, credit amount, and employment length. Employment length is a direct descendant of $G$, hence, the given causal model is not counterfactually fair.

5.2. No Unresolved Discrimination

Definition

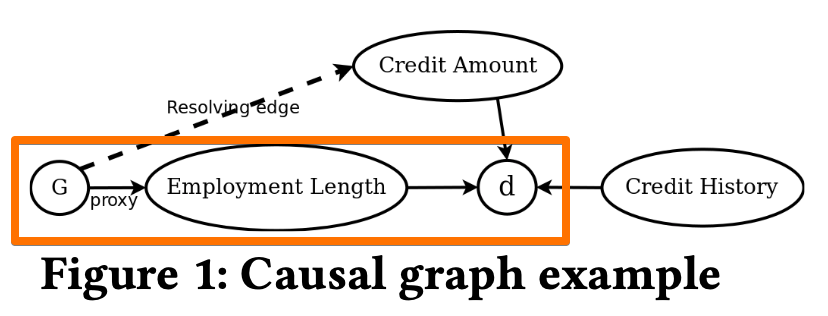
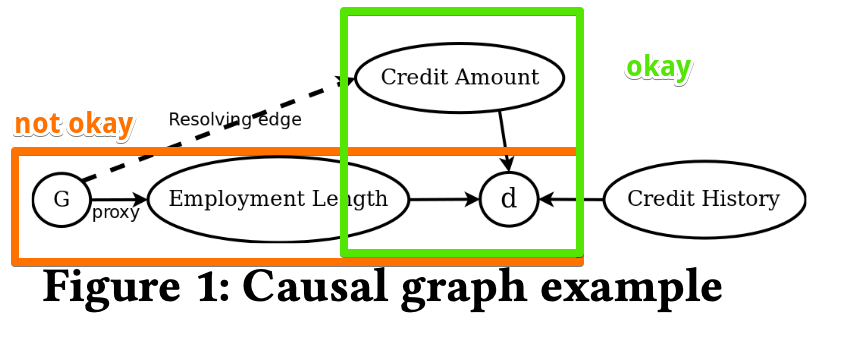
A causal graph has no unresolved discrimination if

  • there exists no path from the protected attribute $G$ to the predicted outcome $d$, except via a resolving variable.

Consequence


© Verma et al.,

  • The path from $G$ to $d$ via credit amount is non-discriminatory as the credit amount is a resolving attribute
  • But, the path via employment length(path from $G$) is discriminatory.
  • Hence, this graph exhibits unresolved discrimination.

5.3. No Proxy Discrimination

Definition

A causal graph is free of proxy discrimination if there exists no path from the protected attribute $G$ to the predicted outcome $d$ that is blocked by a proxy variable.

Consequence


© Verma et al.,

  • There is an indirect path from $G$ to $d$ via proxy attribute employment length.
  • Thus, this graph exhibits proxy discrimination.

5.4. Fair Inference

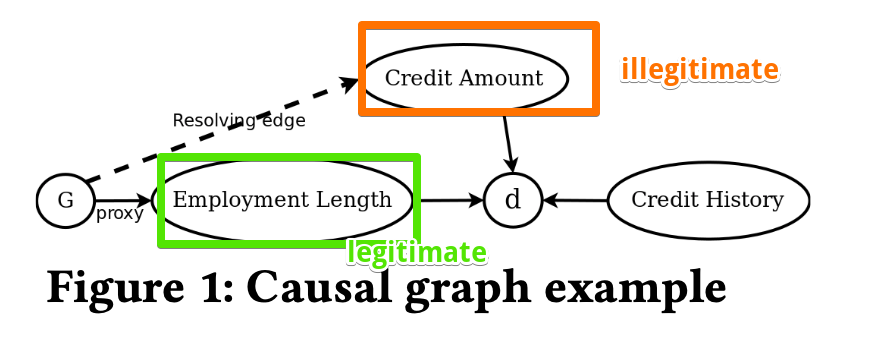
This definition classifies paths in a causal graph as legitimate or illegitimate.

Consequence


© Verma et al.,

  • It might make sense to consider the employment length for making credit related decision.
  • Even though the employment length acts as a proxy for $G$, that path would be considered as legitimate.
  • A causal graph satisfies the notion of fair inference if there are no illegitimate paths from $G$ to $d$, which is not the case in our example as there exist another illegitimate path, via credit amount.

Z. Reference

  • https://online.stat.psu.edu/stat857/node/215/
  • https://fairware.cs.umass.edu/papers/Verma.pdf
  • https://en.wikipedia.org/wiki/Type_I_and_type_II_errors



The End.

2020

[Robot][EN]Hivemapper

2 minute read

Hivemapper,a decentralized mapping network that enables monitoring and autonomous navigation without the need for expensive sensors, aircraft, or satellites.

[CV][GAN][EN]Cycle GAN

8 minute read

Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

Back to top ↑